Whether you’re looking for an excuse to eat dessert or just love mathematics, March 14th is a good day for geeks, nerds, and the rest of the world too. The third month and the fourteenth day, 3.14, is known as Pi day, after the simplest and most ubiquitous constant in nature (no disrespect to c, e, g, or h). Defined as the ratio of a circle’s circumference and it’s diameter, Pi is an irrational number, meaning there is no end to its digits. Most people know 3.14159, but some people have memorized hundreds more digits. Mathematicians armed with supercomputers have calculated Pi to about 12 trillion digits, and those computations took 60 terabytes of data to run.

How does one calculate 12 Trillion digits of Pi? It requires a deep knowledge of mathematics to understand how Pi comes about in nature, and it really helps to be armed with mathematical tools such as an infinite series sum. Gottfried Leibniz, one of the two mathematicians to develop calculus (Newton was the other) found the following simple summation to find Pi.
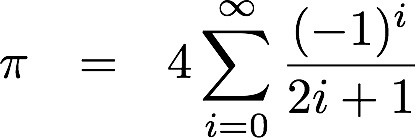
This looks complicated, but it basically means you keep doing the following sum:
1 – (1/3) + (1/5) – (1/7) + (1/9)….
Pretty straightforward, increase the denominator by 2 and alternate the + and – each time. The interesting thing is that the answer keeps going above and below the actual value for Pi as you increase the number of terms. Though each term you add brings it closer to the actual value for Pi. This is called convergence, when a series sum like this reaches a single value. The only problem with the Leibniz formula is that it takes a long time to converge, meaning it’s extremely inefficient and takes up a lot of computer memory to calculate.
Modern mathematicians have found series’ that converge much more quickly to give an estimate of Pi, and they can be a bit more complicated, such as the Chudnovsky formula developed in 1987:
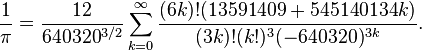
But even though it’s not pretty, it works, producing 14 digits of Pi for every term in the series you add. It was used to calculate Pi to a Billion digits for the first time in history, back in 1989.
But all of the tough calculations aside, Pi is fundamental to our lives. Being an irrational number means that the circumference of a circle is irrational as well. No circle has a definitely calculable circumference, which is really crazy to think about. I’m staring at a coffee cup right now, and I have no way to precisely calculate the distance around it. I can measure it, but it won’t be 100% right. Seems coffee goes well with Pi, and not just with pie.
Thanks for sticking out all the math talk. For reading this far, here’s some pie.

Happy Pie Day! Nom Nom Nom.
